棋牌百科 Q2(停时问题）3苏格拉底的麦穗1骰子2伪概率真排列
Q1: 不停扔色子，直到出现1为止，问最后所有点数的和的期望我的解法：到1为止前面平均我要丢多少次？E次
有1/6概率第一次就丢到1，也有5/6概率第一次不是1，那么我们相当于加一次后从头算起（乘以E+1）平均五次， 
如果是扔到6停呢？还是21因为 
如果是扔到X停，点数和的期望和X是否相关？ 不相关稍微笨一点的解法：
设不拿出来的5个数的均值是x，那么拿出来的那个数就是 
因为我们无论如何都要加单独拿出来的数（sum2），但是前面所有的数丢几次是按概率算的(sum1)：
Q2: 一直生成 (0,1)上的IID的随机数，直到新的数比上一个小就停，问生成随机数个数的期望？我的解法：要知道，如果我们生成n个iid随机数，那么其单调递增排列的概率只有： 
因为他们每个都是iid，可以说，每个都是一样的，我们可以把这个问题类比成n个编号1-n的球(0,1)上随机排列，正好排出1,2,3...n的概率。但是又有一个不同，就是如果第n+1个随机数可以生成，那就意味着前面是已经排好序了，那么新的数可以放的位置的情况只有：| | | | 如图在四根排好序的棍子里再放一根正好是单增的概率是 
。也就是说第n+1个随机数出现的条件概率是 
，它的出现将为随机数个数新增1.于是： 
电脑的解法：电脑不会像我这样联想，但是因为它很能计算，所以我可能打不过它。下面是模拟代码：% 模拟次数
n_trials = 100000;
% 总生成随机数个数s 初始化为0
s = 0;
% 比较x1 x2俩随机数大小
for i =1:n_trials
x1 = rand;
x2 = rand;
t = 2; % 天然就有两个随机数
while x2>x1
t = t+1;
x1 = x2;
x2 = rand;
end
s = s+t;
end
s = s/n_trials;
>> s
s =
2.7189Q3: 假设田里的麦子身高是iid，沿着田路走，试问in expectation要走过多少颗麦子才能见到比第一个麦子高的麦子?（苏格拉底与麦穗的故事）你看到这种，啥分布啥都不给你只给你iid的题，你就要理解，其实啥分布不重要，iid后我们可以当成排列问题才重要。第一个麦子不算数了，那么第二个麦子个子比第一个矮的概率是 
,在第二个比第一个矮的条件下，| | ，第三个比第一个矮的排列的概率 
，依次下来第n个比第一个矮的条件概率是 
。
这种级数其实叫 调和级数（英语：Harmonic series）是一个发散的无穷级数所以in expectation要走过无穷多颗麦子。所以你知道为什么苏格拉底的弟子都失败了吧~第三题和第二题基本上一个思路但是第二题的排列问题是 全排列，第三题的排列问题其实是一个堆，只要第一个是最大即可 所以第二题概率收缩的比较快 最后的平均队长是有穷的第二个概率收缩很慢 是无穷的。补充解释一下调和级数：第三题有读者朋友用代码模拟了一下发现如下情况：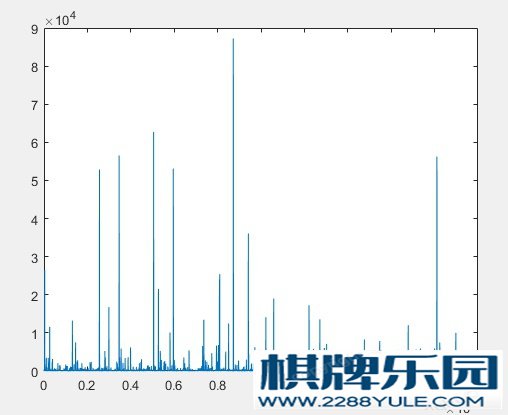
哎？好像不是无穷哎，大部分都在几十以内这种，确实 这就是调和级数的特性啦其实。虽然调和级数随着n趋近于无穷而增加到无穷，但是它增长的很慢。下面是调和级数的增长
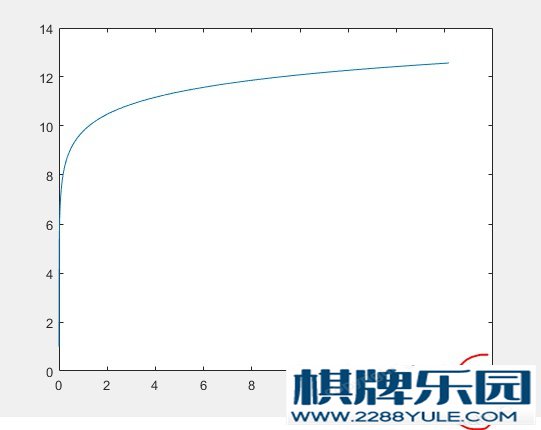返回到我们这个问题，遇到第二颗麦子就比第一颗大的概率是1/2，第三颗才比第一颗大的概率是1/3 * 1/2。那么你就知道，出一个9万步的值的概率有多小啦，所以日常的几十万模拟，是大部分都会在10000以内的。如下图频率分布直方图：
这个问题告诉我们一个什么道理？模拟只对有限的级数的计算可能会有用，但是对于无穷问题，就算是计算机也是不太顶。MATLAB代码放一下：% 这里可以自由决定修改n_trials
function [ s ] = trial(n_trials)
sum_ = 0;
n_trials = 1;
for i = 1:n_trials
x0 = randn;
t = 0;
while randn<=x0
t = t+1;
end
sum_ = sum_+t;
end
sum_ = sum_/n_trials;
s = sum_;
end
a = [];
for i = 1:10000000
s = trial(i);
a = [a,s];
end
掩牌之后西家摸到的第一张牌白板，就是掩牌那一家的和牌。第十巡时，摸进中间牌七筒变成听牌，本来想拆掉白板或八筒，但是白板是掩牌后第一张摸到的牌，考虑到下面的情况，就实在是不能打出去棋牌百科，八筒也是为了应付加番牌而无法随意的就切掉，虽然不敢听牌而拆解掉，但在第十二巡时棋牌百科，虽然是回头也终于变成听牌了。
