点击进入!

（上日报了，谢谢大家厚爱）这个问题很有意思，花10分钟看完这个回答，你可能会从根本上改变你对这个问题的判断和对人生的理解以及顺便学点金融知识一，玩多少次我会妥妥地挂掉？这其实是一个简单的概率学问题百万分之一的发生概率，也就是不发生的概率是99.9999%我们先科普一下，假设A事件发生的概率是40%（那对应不发生的概率就是60%），B事件发生的概率是40%，那么A事件和B事件都发生的概率是多少呢（假设两者是独立事件，两者互不影响）？答案是：40%*40%=16%所以对于一系列独立事件而言，他们都发生的概率就是他们发生的概率的乘积或者，同样的，他们都不发生的概率就是他们各自不发生概率相乘的积。那么，回到这个问题，为了方便我们决策，我们可以先计算出连续尝试若干次（一千次、一万次）而不挂掉的概率是多少，我相信情况会更加明确。假设，我们玩1000次，能够获利5000*1000=5000000，也就是500万元那么玩1000次都不出事儿的概率是多少呢？99.9999%的1000次方，简单用计算器算一下，就可以得出下面这张作死的收益与对应出事儿概率的统计表。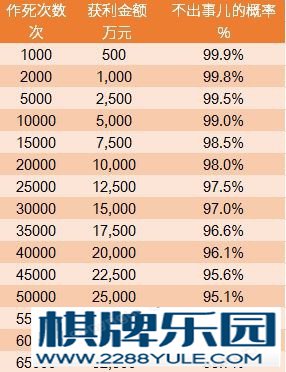可以看到，当我们玩这个游戏1000次时，我们能赚500万元，有99.9%的概率我们还活着因为翻车的这个概率实在太低了，百万分之一所以即使我们往后推算很多次，存活概率依然不小比如我们为了赚2.5亿尝试了5万次时，我们有95%的概率还活着99%和95%其实没有实质性差别，但收益从500万跳涨到了2.5亿那当我们尝试多少次之后，我们的生还概率会低于10%呢？也就是，我们如果连续尝试231万次，次次生还，依然健在的概率只有10%（原文有歧义，已更改），但这个时候，我们已经赚了115.25亿人民币，相当于马云2018年净资产的……6%马云爸爸的钱是真的多啊到底要什么时候急流勇退，悬崖勒马？当然，概率和发生是两回事，这也就是我们金融上所说的风险风险不是指会发生的坏事情，而是指坏事情发生的概率正常情况下，我们所做的所有事情，都是有收益的，不然我们不会去做正所谓天下熙熙，皆为利来；天下攘攘，皆为利往但享受收益的同时，也会有风险人有多大胆，地有多大产就是这个意思就像我们买国债三人斗地主技巧十句口诀，会有利息三人斗地主技巧十句口诀，这是我们的收益；但我们也有本金损失的风险（我国政权灭亡、政府破产），但我国作为一个负责任的大国，这种情况发生的概率微乎其微，可以忽略，所以我们可以视国债的收益为无风险收益但无风险的情况是极少且特殊的，而且因为没有风险，所以收益很低正常情况下，收益越高，风险越大，相信看了上面那张表后，大家会有很直观的感受大家在日常生活中，只要赚取收益，工作也好、存钱也好、买理财也好、买股票衍生品也好都是为了赚取收益，但同时也会衡量风险，只是大家没有这么专业的知识，不会算的很清楚但大家都明白，股市有风险，入市需谨慎。朴素的风险控制意识，大家都有，只是强弱有别。那收益多高算收益高呢？多大风险算风险大呢？不同的人有不同的答案，这个在金融学中有个专业的形容词，叫风险偏好为了便于理解，我们先忽略课本的概念，简化一下对风险偏好的描述。给大家一个直观印象有人讨厌冒险，本能的会规避有风险的投资选择——比如直接不玩这个游戏，这种叫风险厌恶型投资者有人觉得风险和收益匹配的前提下，为了更高的收益冒点风险也值得——比如 @孙瑞昊 的回答，觉得玩1000次，能赚500万，99.9%的概率还活着，那就值得尝试，这是大多数人的状态。这叫风险中性型投资者。当然，有厌恶就有喜好，世界上就有这么一群人，秉持富贵险中求的人生哲学，风险越高，越刺激，越爽，比如——赌徒。对于他们而言，如果收益足够高，哪怕只有10%的胜率，也会去博一次。这就是风险喜好型投资者。所以什么时候急流勇退，金盆洗手，不同的人有不同的答案。三、为什么这个问题下，风险厌恶者这么多？正如题主总结的，原来预估至少90%的人会玩这个游戏但实际上30个回答里有接近一半的人选择了不玩这个游戏这明显不符合我们所说的，风险中性才是大多数人的常态的比例为什么呢？因为对于不同后果，大家会形成不同的风险偏好。比如，如果这个问题的设置是，如果百万分之一的概率会损失所有所得，或者会损失1块钱那么可以预期，大家都会选择玩到自己手断为止但这个题目的不良后果设置是失去生命，对大多数人而言，在失去生命这个结果上，大部分人都是风险厌恶者。只要听到有生命危险，大家都会本能的退避三舍所以，这个比例低于提问者预期，并不奇怪因为大家都不愿意拿自己生命开玩笑，哪怕概率很低很低。四、那要怎么提升大家参与的意愿呢？换个问法就可以就像前面所说的，风险意识大家都有，但是绝大多数非金融经济相关专业的人风险意识都很朴素，对于要承担多大的风险只有很模糊的概念大家不仅对风险没有太具体的概念，对太高的收益也没有太具体的概念#贫穷限制了我的想象系列#一说到“你的生命会有危险”，大家会本能的规避，才会有40%多的答主选择敬而远之但这主要是因为大多数人对于“百万分之一”这个概率，没有直观的认识其实，百万分之一的概率，是非常非常非常非常低了。如果我们把我们日常的事情列一个概率，我们会发现，我们每天都在冒着各种生命危险大多数都不比百万分之一高我们换个问法，如果给你5000块，让你坐一次飞机，你愿意吗？或者给你2500万，让你打的200次，你愿意吗？我相信没有几个人会说不愿意，毕竟，飞机是现目前最安全的交通工具那飞机发生空难的概率是多大呢？最近5年，每百万个航班发生事故的5年均值为0.58次，也就是坐飞机不出事儿的概率是99.999942%——非常接近我们所说的，玩1次出事儿的概率99.9999%遇到空难的概率有多大？也就是说，你玩5000次都不出事儿的概率，和坐5000飞机都不出事儿的概率是几乎一样的而坐车出事儿的概率有多高呢？我们简单粗暴地测算一下根据交通部数据，我国万车死亡率2.2，也就是平均保有量每增加1万辆车，一年就会有2.2人死于交通事故，这还只是1年，是0.022%，按一辆车一年跑300天，一次搭载3人计算，每坐一次车，发生车祸的概率是0.0024%。那坐/开200次车，不发生车祸的概率是99.5%；而这个概率水平，对应到我们前面的表，大概就是2500万，玩5万次所需要承担的风险。如果大家有了这个概念，不参与的比例还会这么低吗？相信不会更不要说，那些擦高层建筑外玻璃墙的、开出租车的、扫大街的、当警察消防的，他们所冒的生命危险，从概率上说，远远高于百万分之一，但他们一辈子都赚不了2500万。我们每天打车、坐地铁、赶公交、炒菜、逛街，这些看似平常的活动，其实都是有一定的概率出人命的，只是这个概率特别特别小，小到我们忽略了但是就算这些概率再小，也不比百万分之一小多少然而，你打车、坐地铁、炒菜、逛街一辈子，能赚2500万吗？2500万什么概念？500万的存款，理财得当就可以衣食无忧（每月躺着拿1万元的投资收益）2500万的存款，光理财收益就可以吊打一线城市95%以上的工薪阶层2500万存银行，4%收益率，一年是100万，存3年就可以在二线城市中心地段全款买房，如果拿来还房贷，可以支撑1400万的房贷，买2000万的房子。上海平均月工资8000多，2500万需要不吃不喝地攒260年。而你需要承担的，只不过是打车200次出事儿的风险一些答主口口声声说，多少钱我都不会拿我的生命开玩笑，拒绝了2500万的诱惑一边每天为了赚几千几万块钱，承受着更高的风险去打车赶公交赶高铁……如果这么一对比，你还会去做吗？反正我就想问——这种游戏在哪儿做？？我能玩到你破产===============更了个新===========评论区很多朋友还是不太能够区分“条件概率”和“独立事件概率”的差别和大家讨论讨论挺有意思的，概率学我也没怎么认真学过，友善探讨互惠互利在这里稍微做一下科普吧，毕竟高中数学隔太久大家忘掉了也正常港真，这玩意儿很抽象，且有的时候反直觉搞混是常事但非有一上来就义正言辞说我错了鄙视我的……昂……大哥你这又是何必……Overconfidence也是金融学的大忌好么……就拿高大上的伯努利试验（其实就是扔钢镚儿看正反面，伯努利这哥们儿叫的早，所以以他命名，占了个年纪大的便宜）来举例吧。伯努利大哥扔了N多次硬币后，得出的结论是——不管之前扔了多少次，下一次的概率依然是正面50%，反面50%，哪怕前面扔的1000次，都是奇迹般地正面朝上，第1001次扔硬币，出现反面的概率仍然是50%。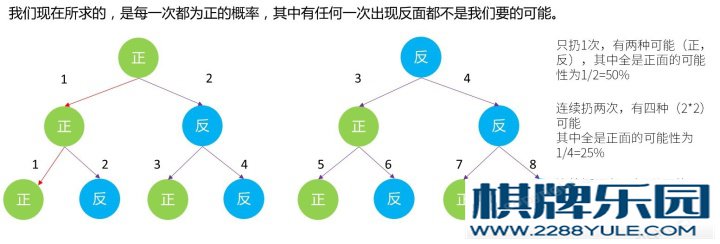简单的说，第一次和之后1万次、一亿次的扔硬币结果都是互不影响的，每一次扔硬币硬它都有自己的想法，大家是相互独立的，这是独立事件概率但我们现在所要求的，不是独立事件的概率，而是由独立事件组成的连续事件中某个特定组合发生的概率这完全就是两回事这里我们用经典的二叉树模型做一次推导，为了简洁，我们只看连续扔三次，可能出现多少种情况（实际上是因为我懒）第一次扔，有（正）（反）两种可能，各50%第二次扔，有（正，正）（正，反）（反，正）（反，反）4种可能，这个时候连续两次为正的概率就只有4种中的1种，即25%第三次扔，已经有了2的3次方也就是8种，分别为（正，正，正）（正，正，反）（正，反，正）（正，反，反）（反，正，正）（反，正，反）（反，反，正）（反，反，反），可以看到，连续三次为正的情况，在8种中只有1种，可能性是1/8=12.5%如果正是生，反是死，那不管是3个人同时扔色子都活着，还是1个人扔了三次之后还活着的概率，都是12.5%所以独立事件发生的概率不受之前发生的事情结果影响但当所求的事件概率为一系列独立事件构成的整体事件中，某一条件发生的概率时，就需要叠加前面事件的概率，因为这是这个游戏仍然能继续进行的前提比如本问题中，要赚2.5个亿，那就是连续5000次都生还的概率的乘积，中间任何一次，出现了没有生还的事件，都会让游戏者当场去世。那可能性就只有一种，就是5000次都生还，只有第一次，第二次都生还了，才有后续的可能。所以，连续生存5000轮，和连续生存2轮，存活率自然是不一样的。有的答主非常机智，说，那我玩完100次之后，我决定不干，骗一下概率然后我突然！决定再玩！概率不就重置变回百万分之一了吗？？欺骗一时爽，一直欺骗一直爽可是……你之前玩的那100次，虽然都活了下来，但每次都积累了挂掉的概率啊……你之所以玩了100次还能欺骗概率，欺骗硬币和伯努利，是因为你运气好玩了100次都没挂啊，风险并不会因为没有发生就消弭，也不会因为发生了之后就一路坦途，虽然可能有点反常识，但想要欺骗概率，恐怕不行。其实，不管你骗不骗，你每次玩游戏，新开的那一局的概率都是百万分之一，不会变的……而我们所追求的，每次玩都不出事的概率，随着游戏次数的增多，也还是不断变小的。==============再更个新============打个广告，我们正在酝酿一个趣味科普经济学、金融学知识的公众号用最直白的语言，最有趣的案例，让冰冷的专业术语不再陌生每周三、周六更新，预计公众号将于2019年6月上线届时，欢迎大家关注和支持，和我们一起互动如果有插画技能的同学想要加盟，也可以在评论区和我们联系成为原始股东的机会窗口期即将结束，希望能在这之前，遇见你。感谢大家的热爱笔芯~============公众号福利=========经过了半年的筹备，我们的财经科普公众号——橘猫财经已经正式上线啦！这里没有高大上的公式，没有复杂的模型只有最直白的大白话，最生动日常的例子还有一只胖橘猫，陪伴着你。关注我们，我们的故事就开始了。微信搜索“橘猫财经”或直接点击下方链接，来到我们的身边猫主人期待您的光临！