点击进入!

一、解决排列组合综合性问题的一般过程如下：1、认真审题弄清要做什么事；2、怎样做才能完成所要做的事，即采取分步还是分类,或是分步与分类同时进行，确定分多少步及多少类；3、确定每一步或每一类是排列问题(有序)还是组合(无序)问题，元素总数是多少及取出多少个元素；4、解决排列组合综合性问题，往往类与步交叉，因此必须掌握一些常用的解题策略。小结：“16字方针”：分类相加，分步相乘，有序排列，无序组合。本章知识结构网络图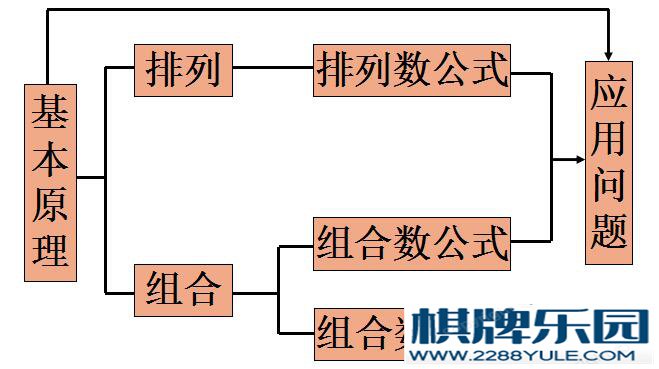两个基本计数原理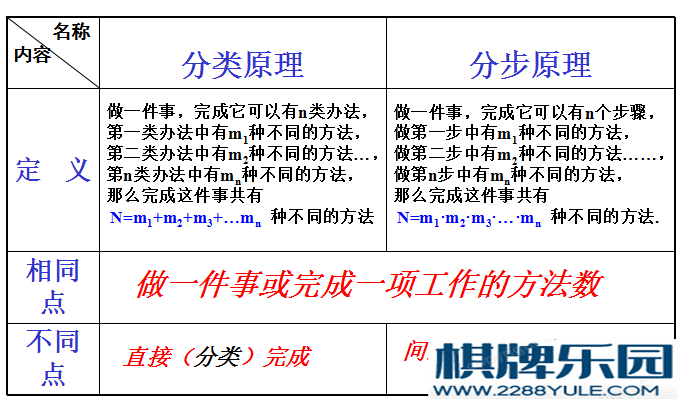：排列和组合的区别与联系：二、基本题型讲解1、特殊元素和特殊位置问题例1：（1）从8个人的数学兴趣小组中选两人分别担任正、副班长的不同方法种数。分析：这是无限制条件的排列，显然方法种数是。（2）由0，1，2，3，4，5可以组成多少个没有重复数字的五位数奇数。分析：这是有限制条件的排列，由于末位和首位有特殊要求，应该优先安排，以免不合要求的元素占了这两个位置。TIP:特殊元素和特殊位置优先策略：一般先考虑特殊元素，再考虑其它元素。若以元素分析为主,需先安排特殊元素,再处理其它元素.若以位置分析为主,需先满足特殊位置的要求,再处理其它位置。若有多个约束条件，往往是考虑一个约束条件的同时还要兼顾其它条件。做到不重不漏。三、相邻相间问题1、相邻元素捆绑策略例2：7人站成一排，其中甲乙相邻且丙丁相邻，共有多少种不同的排法。分析：可先将甲乙两元素捆绑成整体并看成一个复合元素，同时丙丁也看成一个复合元素，再与其它元素进行排列，同时对相邻元素内部进行自排。由分步计数原理可得共有种不同的排法。TIP：捆绑法，要求某几个元素必须排在一起的问题，可以用捆绑法来解决问题，即将需要相邻的元素合并为一个元素，再与其它元素一起排列，同时要注意合并元素内部也必须排列。2、不相邻问题插空策略例3：7人站成一排，如果甲乙必须不相邻，那么不同的排法种数？分析：除甲乙外，其余5个排列数为种，再用甲乙去插6个空位有种，不同的排法种数是=3600.例4、某班要排毕业晚会的节目顺序，有4个音乐节目、2个舞蹈节目和1个曲艺节目，要求2个舞蹈节目不连排，不同的排法是？=3600.TIP：插空法，对于某几个元素不相邻的排列问题，可先将其它元素排好，然后将不相邻的元素在已排好的元素之间及两端的空隙之间插入即可。3、元素定序问题例5：7人排队，其中甲乙丙3人顺序一定共有多少不同的排法？分析：(倍缩法)对于某几个元素顺序一定的排列问题，可先把这几个元素与其他元素一起进行排列，然后用总排列数除以这几个元素之间的全排列数，则共有不同排法种数是：种方法。 (空位法)设想有7把椅子让除甲乙丙以外的四人就坐共有种方法，其余的三个位置甲乙丙共有1种坐法，则共有种方法。TIP：一般用除法处理，即n个元素的全排列中若有m个元素必须按照一定顺序排列，这m个元素相邻或不相邻不受限制，其排列数为4、重排问题求幂策略重复排列问题要区分两类元素：一类是可重复，另一类不能重复，把不重复的元素看作“店”，能重复的元素看作“客”，则通过“住店法”可顺利解题，在这类问题使用住店处理的策略中，关键是在正确判断哪个底数，哪个是指数 。例6： 8名同学争夺3项冠军，获得冠军的可能性有多少种？分析：对于同一项冠军，学生不能重复，但同一个学生可获得多项冠军，把8名学生看作8家“店”，3项冠 军看作3个“客”，他们都可能住进任意一家“店”，每个“客”有8种可能，因此共有种不同的结果。小结：不可重复的当作底数，可重复的当做指数。练习：（1）有4名学生报名参加数学、物理、化学竞赛，每人限报一科，有多少种不同的报名方法？ （2）有4名学生参加争夺数学、物理、化学竞赛冠军，有多少种不同的结果？ （3）将3封不同的信投入4个不同的邮筒，则有多少种不同投法？解：（1）（2）（3）你都答对了吗？未完待续，请期待2.0破解版——平均分配Inner peace~

然后，还要有好的心态棋牌百科，毕竟欲速则不达，四川麻将、麻将游戏、麻将技巧、打麻将必胜绝技想急于求成时最不可取的。

其次，二人麻将还有不少细节。比如，必须先打中发白，出牌没有做三元的可能；杠牌的时候尽量谨慎，万子能不杠就不杠，为的是不暴露自己的牌型，因为一旦杠了什么牌，然后打几张后就能猜出一二了。对手听牌的时候，一般是对家打4万，1万棋牌百科，7万相对比较安全，基本上按147，258，369的节奏相对安全。有时宁可不要叫，毕竟不查叫的。